Solving the sums of risk hedging The stochastic differential equation that revolutionized the financial markets
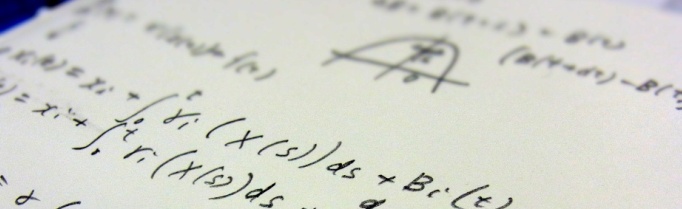
Besides stocks, bonds and currencies, a bevy of financial derivatives ? futures, options and swaps, among others ? are traded in today’s financial markets. Moreover, new financial products are constantly being developed, behind which is market participants’ desire to minimize or hedge against losses from the uncertainty inherent in existing products. The Black-Scholes (BS) financial model was devised to help reduce such uncertainty and was first used to set pricing of European-style stock options.1
A European option refers to a variety of financial contracts, including stock and foreign exchange transactions. In any of these trades option buyers can hold losses in check, but the seller is more exposed to potentially heavy losses. Black and Scholes tackled the question of how to set a fair selling price, or premium, of a European stock option.
Black and Scholes devised their model for a portfolio of one stock and one bond,2 in which the stock price (S) and the bond price (B) satisfy the Black and Scholes Equation (Eq.1). As long as the stock and bond prices move obey the model, the authors argued that by way of daily stock transactions the seller can replicate what the buyer would earn through exercising an option.
In other words, if the shares and bonds held in the hedging portfolio are fully sold off when the option is exercised, the seller can recover an amount of money (asset value) equal to the option exercise price, and therefore is provided with a replicating or hedging stock transaction strategy. In devising this strategy, Black and Scholes established the Black and Scholes option pricing formula (Eq.2) to determine the initial funds required and designated this amount the premium.
“The BS theory was epoch-making in that it created a means of hedging against risks by diffusing option-contract risks through stock transactions,” says Shigeo Kusuoka, a professor of the Graduate School of Mathematical Sciences at the University of Tokyo. Today, this approach is known as the dynamic hedge, or portfolio strategy.

Kiyoshi Ito (1915-2008)
Alma mater: Tokyo Imperial University (predecessor of the University of Tokyo), Department of Sciences - Mathematics Degree: Ph.D
Institutions: Professor of Kyoto University. Aarhus University (Denmark), Cornell University etc.
Fields: Theoretical studies on stochastic differential equations and stochastic integration
Known for: role in establishing the bases of stochastic calculus
Major awards: Wolf Prize (1987), Kyoto Prize (1998), Carl Friedrich Gauss Prize (2006), Medal for Cultural Merits (2008)
(Photo: IMU Carl Friedrich Gauss Prize, August 2006)
A mathematical representation of Brownian motion is employed to describe continuously and randomly-fluctuating stochastic processes such as stock prices. The first person to accurately depict mathematically a random process developing over time and with noise was Kiyoshi Ito, describing Brownian motion in a stochastic differential equation.
In the 1980s, it became clear that the concept of replication could be applied to a range of financial derivatives, and, as with the BS model, they were all represented with stochastic differential equations, demonstrating the concept’s viability.
“Professor Ito is unquestionably the father of the stochastic differential equation,” says Kusuoka. “Finance is just one of its applications, although this was not his intention at all.” Indeed, because the equation was initially used in analyzing stock prices, Kusuoka says that many people in financial circles in the United States and Europe long thought Ito the mathematician to be an economist.
to solve Stochastic Differential Equations
The BS model, while revolutionary, proved not to be fully consistent with market realities. Other models followed in efforts to establish better ways to reflect reality. Yet, a model is supposed to be accurate and predict an outcome at the same time. A model that cannot provide an outcome with some accuracy is of little practical use.
Finding numerical solutions to differential equations has long been a major theme in mathematics, but efforts to solve stochastic differential equations have only just begun. Kusuoka, who leads the way in this field, has proposed a new method known as the “Kusuoka Approximation.”
The principal methods for solving ordinary differential equations with a single variable are Euler’s method and Taylor’s method. The Euler-Maruyama method, which employs Euler’s method, is widely used to solve stochastic differential equations but is not very accurate.
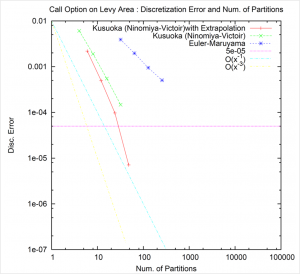
Fig1. Discretization error and number of partitions
Both Kusuoka’s approximation and the Euler-Maruyama method are discrete approximation methods.
As a continuous-time formula the stochastic differential equation is difficult to work with, so the axis of time is divided into discrete sections and an approximation calculated.
The relationship between the number of divided sections and the margin of error, as found in numerical experiments, show that Kusuoka’s method excels Euler-Maruyama method in accuracy and promises to be still more accurate if an extrapolation method is employed.
There is also a problem employing Taylor’s method to solve stochastic differential equations, as it requires the repeated stochastic integration of Brownian motion. Because the probability distribution of this integration is unknown, calculations become impossible.
So Kusuoka has proposed his own method, of which he says, “We don’t need to know the probability distribution exactly. If the distribution satisfies certain conditions, then we can use a highly accurate approximation incorporating Taylor’s method.” To prove the accuracy of his scheme, however, is very difficult. Kusuoka notes that, “Only a few researchers really understand it. Still, it has practical applications.”
Kusuoka’s approximation has been supported by a series of numerical experiments (Fig.1). Hoping to have his method used by people in the financial industry, Kusuoka has developed a computer program in collaboration with Shoichi Ninomiya, a professor of the Graduate School of Innovation Management at the Tokyo Institute of Technology, and Mariko Ninomiya, a research associate of the University of Tokyo’s Graduate School of Economics. Their work was posted on the Internet in December 2011. [https://sites.google.com/site/marikoninomiya/]
Of his method, Kusuoka says, “Some people may come across problems with my method in certain situations. I look forward to any comments.” Even so, it seems that in the meantime his attention is focused on finding a solution to barrier-option derivatives, his new research theme.
1A European option is a contract that confers the right (option) to purchase or sell an item at a pre-determined price or rate on a fixed date.
2A collection or combination of risk-free and risky assets used as a means of diversifying investments and thereby hedging against risk. In the BS model a bond is a risk-free asset and a stock is a risky (speculative) asset.
Acknowledgment

Professor Shigeo Kusuoka, Graduate School of Mathematical Science



![[equation 1] Black and Scholes equation [equation 1] Black and Scholes equation](/content/400020987.png)