深層学習によるデータ固有のフラクタル構造などへの適応を証明
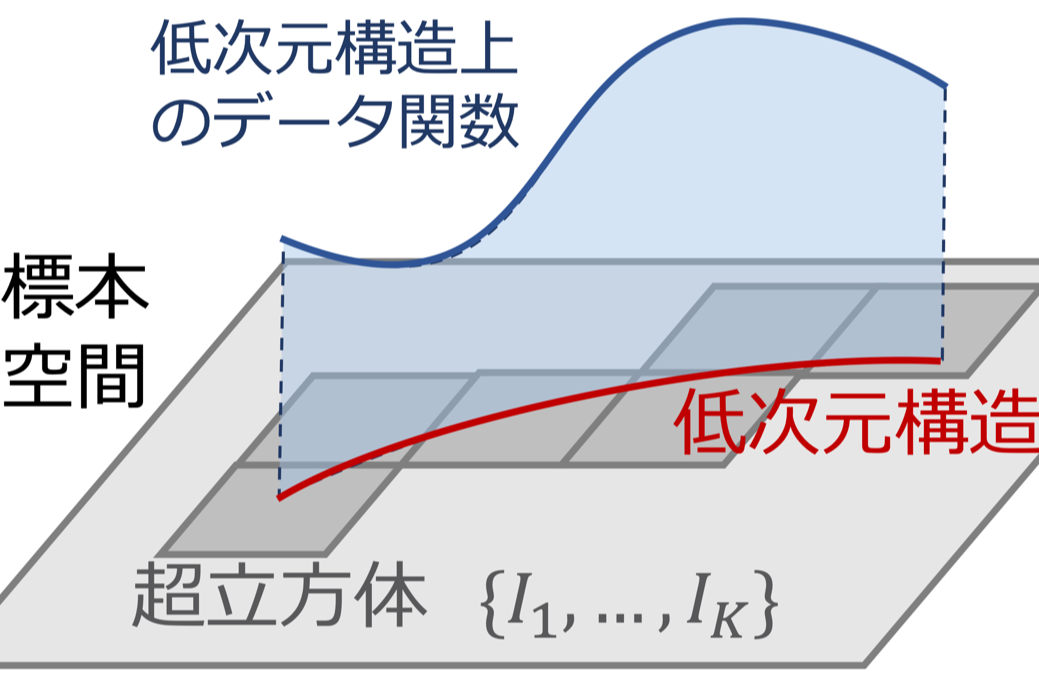
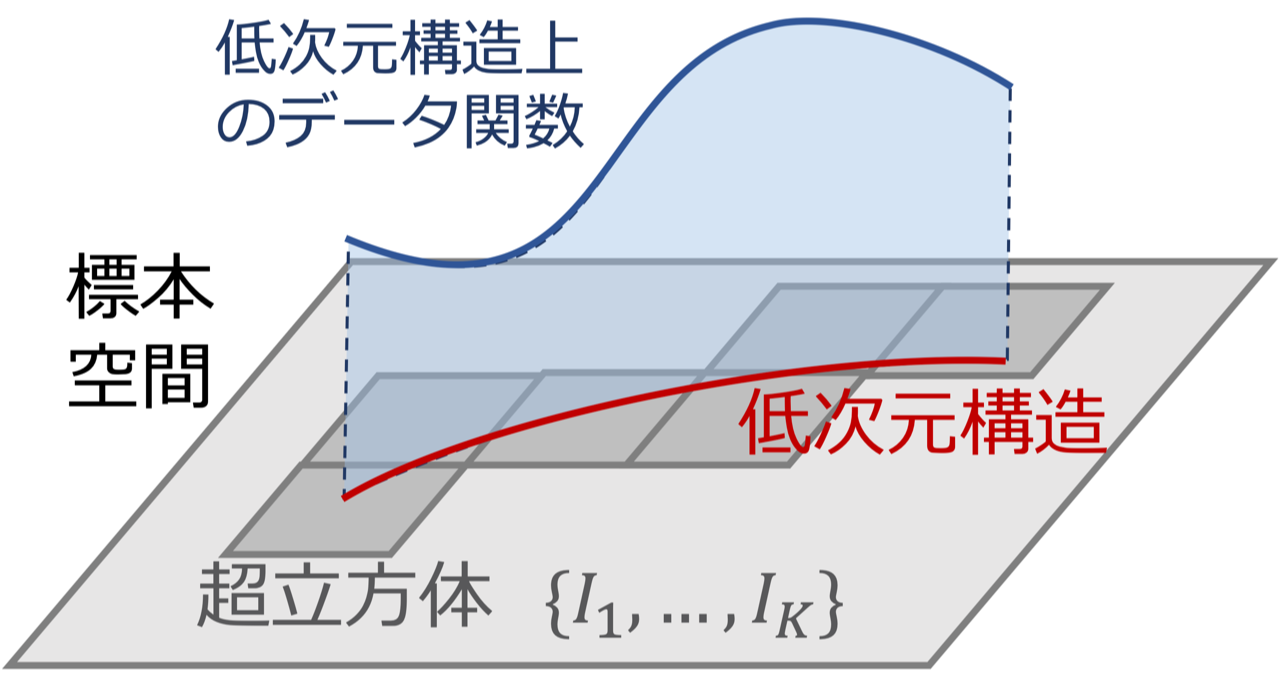 証明の模式図
証明の模式図 東京大学大学院総合文化研究科附属先進科学研究機構の今泉允聡准教授、アメリカ・ラトガース大学統計学科博士課程の中田竜明氏による研究チームは、深層学習による予測誤差の大きさを数学的に解析しました。その結果、深層学習がデータの中に隠れているフラクタルなどの低次元構造に適応し、その次元の大きさに応じて誤差を減少させられることを数学的に証明しました。なお、深層学習以外のデータ解析手法も、データのシンプルな低次元構造に適応できることが既に証明されていますが、本研究が構築した理論では、深層学習ならば通常の構造だけでなく、フラクタル構造などの複雑な形状にも適応できることが明らかになりました。
深層学習は高い性能を発揮するデータ解析法ですが、その原理には不明な点が多く残っています。この原理を明らかにする上で重要なのが、データの持つ「隠れた低次元構造」です。深層学習が扱うデータの多くは、表面上からは発見できない低次元構造を隠し持っています。現代的なデータ解析手法の多くはこの低次元構造に適応することで、予測精度を向上させていることが経験的に知られています。理論的には、深層学習以外のデータ解析手法もシンプルな低次元構造には適応できることがすでに証明されています。しかし、深層学習はこれらの方法より高い性能を実験的に発揮するため、この実験結果を説明するにはより発展的な理論が必要でした。
研究チームは、深層学習による回帰問題(教師あり学習の一種)の予測誤差を数学的に解析し、データ数の増加による予測誤差の改善スピードが、データの表面的な次元には影響されず、代わりにデータ固有の低次元構造の次元(固有次元)によって決まっていることを数学的に証明しました。すなわち、どんなに高次元なデータであっても、そこに隠れている構造が低次元であるなら、深層学習はデータが低次元の場合と同様の高い精度を発揮することが証明されました。さらに、深層学習はこの低次元構造がフラクタルなどの複雑な形状を持っている場合でも、それに応じた固有次元に適応できることが明らかになりました。これは、深層学習以外の方法では示されておらず、深層学習が低次元構造への適応という文脈で、他手法に対する優位性を持つ可能性が示唆されました。
深層学習は優れたデータ解析手法ですが、計算コストが大きいなどの実用上の問題点が残っています。本研究の成果は、データの構造に適応したコンパクトなニューラルネットワーク設計を行うなどの、計算コストを削減する運用法の開発に役立つと考えられます。
「深層学習の性能について未解明の点はまだまだ多く、今後も多くの研究を続ける必要があります」と今泉准教授は話します。
論文情報
Ryumei Nakada, Masaaki Imaizumi, "Adaptive Approximation and Generalization of Deep Neural Network with Intrinsic Dimensionality," Journal of Machine Learning Research 21(174):1-38, 2020: 2020年9月20日
論文へのリンク (掲載誌 )
)