リスクヘッジを解く 金融市場を一変させた確率微分方程式
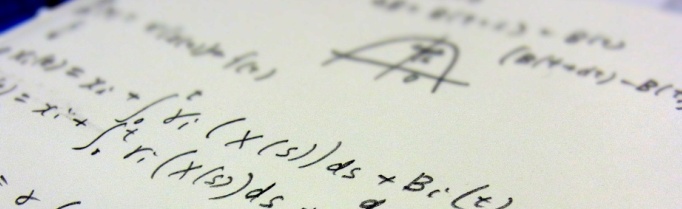
金融市場には、株式、債券、為替といったものだけでなく、先物、オプション、スワップなどさまざまな金融派生商品(デリバティブ)があります。「明日はどうなるか分からない」という金融商品の不確実性からくる不利益をなるべく減らそう(リスクヘッジ)という視点から、さまざまな商品が開発されてきました。ブラック・ショールズモデル(以下BSモデル)は、その中でも株のヨーロピアン・オプション(注1)を扱っています。
ヨーロピアン・オプションには、株や為替などいろいろあります。いずれの場合も、オプションを買った側は損を抑えられますが、売った金融機関は大きな損を抱え込むことがあります。こういう状況の中で、ブラックとショールズは、「株のヨーロピアン・オプションの売買価格(プレミアム)をどう決めたらよいか」という問題に取り組みました。
彼らは1銘柄の株と1種の債券からなるポートフォリオ(*2)を対象とし、株価(S)と債権価格(B)が式1を満たすBSモデルを考えました。そして、株価と債券がBSモデルに従っている限り、売り手は株の日々の売買によって、買い手がオプションを行使した場合と同じものを作り出す(複製)ことができることを示しました。つまり、オプション行使日にすべての株と債券を処理すると、手元に残る金額(資産価値)がオプションの行使価格と同じになる株の売買戦略が存在するのです。その戦略をとる時に、最初に要する資金がいくらかを求める公式(式2)を導き出し、これをプレミアムとしました。
「彼らの理論は、株の売買を通してオプションのリスクを市場に流せるという、それまで誰も知らなかったリスクヘッジの方法を発明した点で非常に画期的なものです」と、東京大学大学院数理科学研究科の楠岡成雄教授はいいます。この手法は、今では、動的ヘッジ戦略(動的ポートフォリオ戦略)とよばれています。
株価のように刻一刻変化し、その動向がランダムなものの確率過程を記述するには、ブラウン運動を数理化したものを用います。ノイズとともに発展していくランダムな過程を、ブラウン運動を取り入れた確率微分方程式として、初めて数学的に正確に表現したのが伊藤清でした。

伊藤 清(いとう・きよし)
1915~2008年。東京帝国大学(東京大学の前身)理学部数学科を卒業し、1945年に同大学から理学博士号を授与される。京都大学教授、米国のプリンストン高等研究所研究員、スタンフォード大学教授、デンマーク・オーフス大学教授、米国コーネル大学教授などを歴任。確率微分方程式・確率積分の理論を中心に確率解析学を確立した功績により、ウルフ賞(1987年)、京都賞(1998年)、ガウス賞(2006年)、文化勲章(2008年)などを受賞。
写真:(IMUガウス賞受賞記念。2006年8月撮影)
BSモデルも確率微分方程式で表されています。BSの複製理論に数学的な証明を与えたのは、米国の経済学者R・マートンです。BSモデルでは資産価値が確率積分で表されることに気づき、伊藤の公式を使えば、複製の方程式を解くことができることを示したのです。この公式は、確率微分方程式の式変形を進めるために伊藤が考え出した手法で、これを使えば容易にある種の微分方程式を解くことができます。
1980年代に入ると、さまざまな金融商品のいろいろなデリバティブに対して、複製の考えが適用できることが明らかになりました。どのモデルもBSモデルと同じように確率微分方程式で表されています。だからこそ複製が可能だといえます。
「伊藤先生は、まさに確率微分方程式の開祖で、その応用分野の1つが金融だったわけです。ご自身はまったくあずかり知らぬことだったのですが…」と楠岡教授。欧米の
金融関係の人の中には、伊藤を経済学者だと思っていた人が大勢いたといいます。
BSモデルは画期的でしたが、市場との齟齬もいろいろありました。そこで、できるだけ現実を反映する正しいモデルを求めて、いろいろなものがつくられてきました。
しかし、モデルは正しいだけでなく、解けることも非常に重要です。解けないモデルは絵に描いた餅にすぎません。
微分方程式の数値解法は長らく数学の研究テーマになってきましたが、確率微分方程式の解法ともなると、まだ手がついたばかりです。楠岡教授はその研究を行っており、「楠岡近似」と呼ばれる新しい手法を提唱しています。
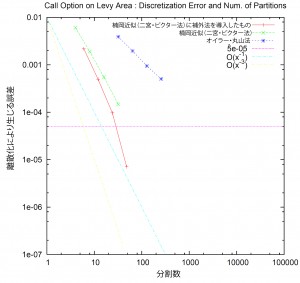
図1 数値実験による分割数と誤差の関係
楠岡近似もオイラー・丸山法も離散近似法である。確率微分方程式は連続時間の方程式であるが、そのままでは取り扱いが難しいので、時間の区間を分割して時間を離散化し、近似計算を行う。数値実験での分割数と誤差の関係を見ると、オイラー・丸山法より楠岡近似の精度が高く、楠岡近似に補外法を導入するとさらに精度が高くなることがわかる。
常微分方程式(変数が1種類の微分方程式)の解法として、オイラー法とテイラー法があります。オイラー法を確率微分方程式の解法に取り入れたのが、オイラー・丸山法です。 非常によく使われていますが、精度が高くありません。 一方、テイラー法を取り入れるには難題がありました。確率微分方程式に取り入れると、ブラウン運動の確率積分が何回も出てきます。現在のところそういうものの分布がまったく分かっていないため計算不能になってしまうのです。
それに対して楠岡教授は、「正確な分布を知る必要はない。分布がある条件を満たしていれば、テイラー法を導入して精度の高い近似ができる」という枠組みを示しました。その証明は非常に難しいもので、楠岡教授いわく、「この分野でもほんの一部の人にしか理解されていません。しかし、実用性はあるのです」。
数値実験でも非常に良い近似だということが示されています(図1)。そこで、金融の現場の人たちに実際に使ってもらおうと、東京工業大学の二宮祥一教授、本学経済学研究科の二宮真理子特任助教と組んでプログラム化をはかりました。昨年12月からこちらのサイトで公開しています。
「いろいろな人が使えば、『こういう場合にはちょっと問題がある』といったことも出てくるでしょう。それも楽しみです」といいつつも、もはや楠岡教授の頭は、現在挑戦中の新しい課題、「バリアー条件付きデリバティブの解法」に占められているようです。
取材協力

楠岡成雄教授 大学院数理科学研究科