千字で語るコロナ論|数理生物学 大橋 順|コロナ禍と東大。

千字で語るコロナ論
東京大学が擁する全26部局から十人の研究者を選び、自身の専門分野の視点からコロナ禍について千字で執筆するよう依頼しました。それはコロナ禍を通して自身の研究を綴るという試みでもあるでしょう。2020年夏、東大研究者たちは何を思い、考えていたのか?
コロナ禍について語るときに研究者の語ることとは?
千×十の計一万字でお届けします。

新型コロナウイルス感染症の数理モデル

理学系研究科 准教授
新型コロナウイルス感染症が地球規模で拡大しています。ワクチンや治療薬が開発されるまで、感染者が爆発的に増えることのないような対策をたてる必要があります。ここで活躍するのが数理モデルです。数理モデルとは、方程式によって様々な現象を数学的に記述したモデルのことを言います。感染症の数理モデルは連立微分方程式によって記述され、解析的に解くことが難しいモデルでも数値計算であれば表計算ソフトで簡単に行うことができます。
全く対策を取らなかった場合に1人の感染者からうまれる2次感染者は2.5人であると仮定し(中国・武漢での推定値)、集団中の個体を感受性者(S)、潜伏期感染者(E)、発症者(I)、回復者(R)の4つに区分したSEIRモデルを用いて、新型コロナウイルス感染者数の時間変化を計算しました。その結果、5か月後に発症者数がピークを迎え、そのピーク時には人口の15%くらいの人が発症しているという制御不能な状態となることがわかりました。一方、他者との接触頻度を現在の40%以下に保ち続ければ感染は拡がらず、45%程度を保った場合であってもピークを2年以上先まで遅らせることが可能であることがわかりました。
感染症にかかると、人の体内ではそのウイルスや細菌などの病原体を排除するための抗体がつくられます。このようなシステムを免疫といいます。ワクチン接種を受けると、この免疫システムが事前に抗体をつくり、感染を予防することができます。麻疹ウイルスの場合は、一度感染すると二度と感染しないように免疫システムが働きます。これを終生免疫といいます。しかし、一般的なコロナウイルスやインフルエンザウイルスに対して人は終生免疫を獲得することができません。新型コロナウイルスに対しても獲得は出来ないと考えられています。既感染者の体内から新型コロナウイルスに対する抗体が数か月で消失することも報告されています。終生免疫を獲得できなければ何度も感染し発症する可能性があります。免疫が平均1年で消失すると仮定して数理モデル(SEIRSモデル)を用いて計算すると、ある程度の対策をとっていても複数回流行のピークを迎えた末、人口の1%程度の人が常に発症している平衡状態に陥ることがわかります(図)。この結果からも、ワクチン開発が急務であることが理解できます。感染症の数理モデルはわれわれに多くのことを教えてくれるのです。
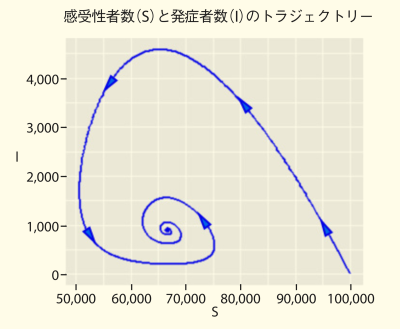
※SはSusceptible、EはExposed、IはInfectious、RはRecovered