Group Theory and Its Applications: Introduction to beautiful modern mathematics

I graduated from the Department of Mathematics of Nagoya University and Graduate School of Mathematical Sciences of the University of Tokyo. I have been an Assistant Professor at Tokyo Metropolitan University, an Associate Professor at Nagoya University and I became a Professor of Kavli IPMU in 2017. During these times, I visited University of Warwick (UK), University of Mannheim (Germany), Institute of Advanced Study (Princeton, US), Newton Institute (Cambridge, UK) and so on. I received the Special Takebe Prize from the Mathematical Society of Japan in 2001 for my research on crepant resolution and the McKay correspondence. I am also a member of the Science Council of Japan and also a Professor of the Ohara Ikebana school.

Prof. Yukari Itoh

1	Subject	Group Theory and Its Applications: Introduction to Beautiful Modern Mathematics
2	Field	Algebra
3	Key words	Group, Symmetry, Ring, Algebraic Geometry, Singularity, McKay correspondence
4	Global Unit	1
5	Lecturer	Yukari Ito
6	Period	July 3 - 14, 2023
7	Time	10:30am-12:00noon (Japan Standard Time)
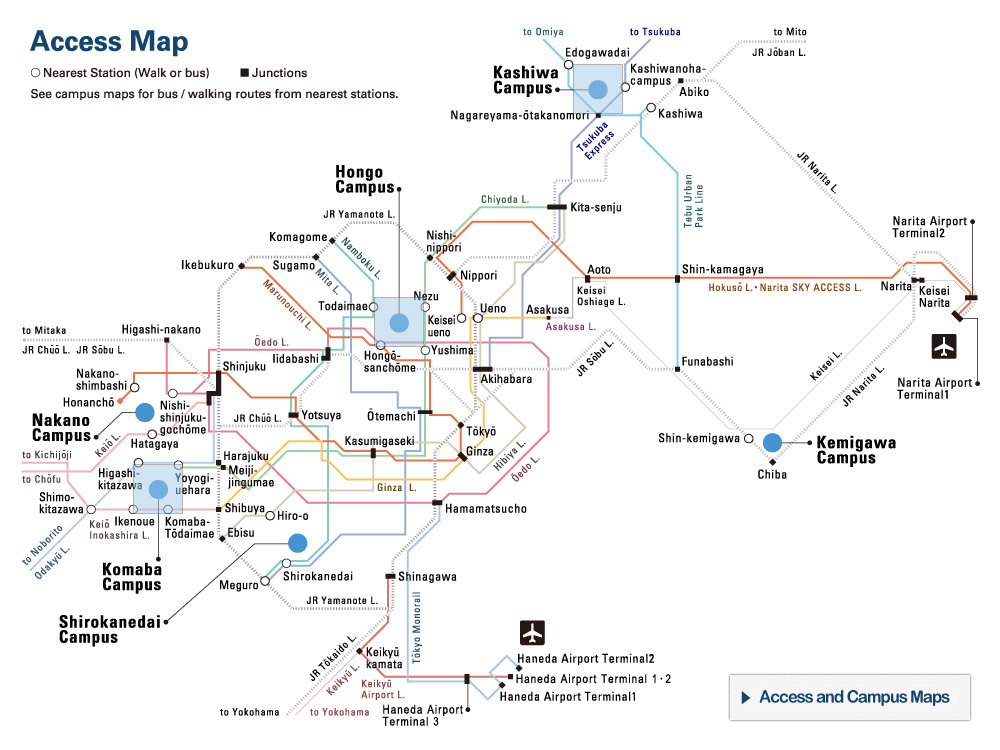
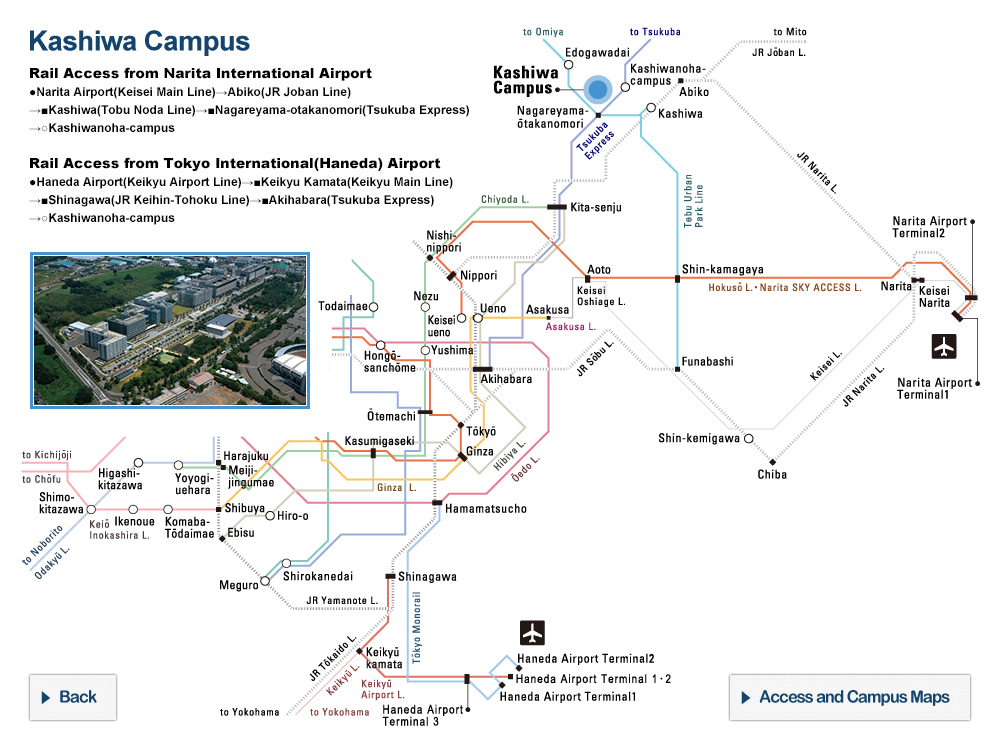
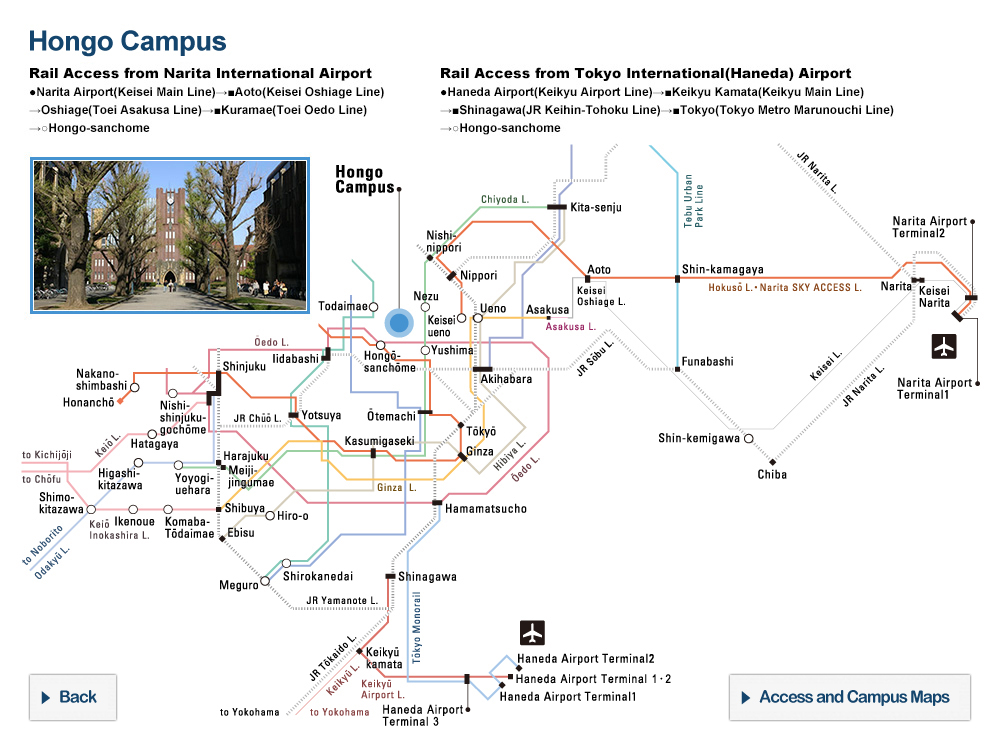
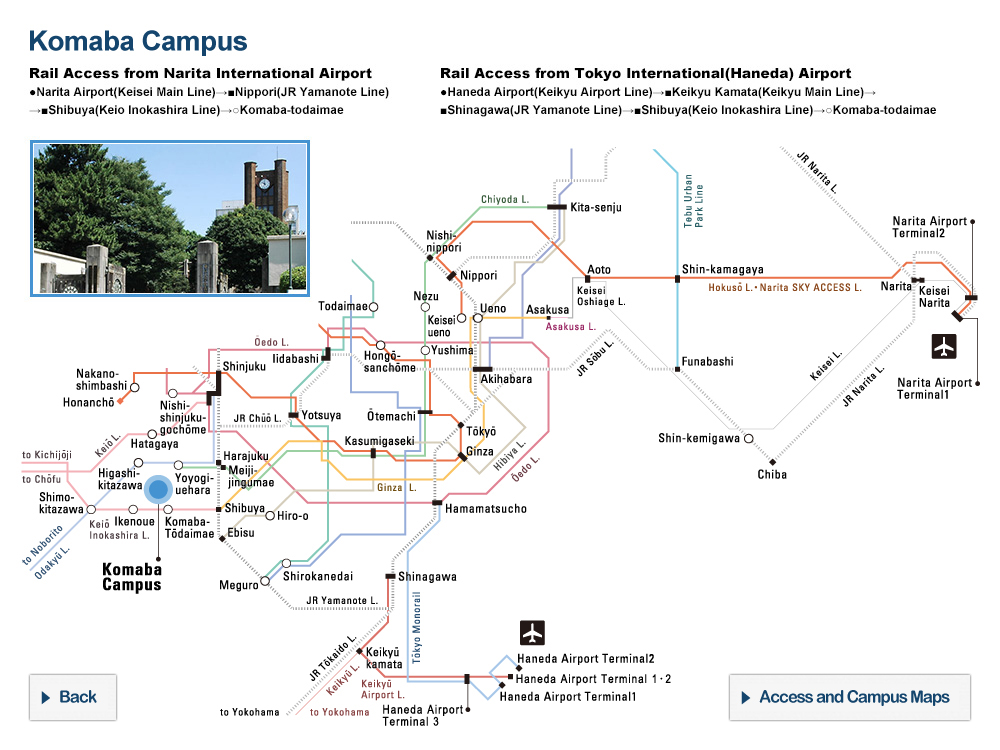
8	Lecture style	In-person (on Hongo Campus)
9	Evaluation Criteria	Excellent (S) 90 –100％; Very good (A) 80–89％; Good (B) 70–79%; Pass (C) 60–69%; Fail (D) 0–59％
10	Evaluation methods	We will have small exercise during the lectures and report after all lectures. I will check both of them.
11	Prerequisites	If you are interested in mathematics, in particular, algebra, you are welcome to this lecture. If you know something about basic algebra like group, polynomial ring, then it will be easy to understand this lecture. However I will introduce every definition during lectures and I don't assume any knowledge on algebra.
12	Contents	Purpose By this course, you can learn most basic Group theory, the geometrical meaning and some applications to Geometry. Moreover, we will tell you some examples of Groups in Japanese culture. Description Each lecture contains lecture and exercise. The contents of the lectures consist from Group Theory, Representation theory of finite groups, Introductive Algebraic Geometry and singularities. I would like to introduce recent research related with group theory like McKay correspondence. I am planning to teach following contents in this lecture: Schedule 1) Introduction to Algebra 2) Definition of Group 3) Normal subgroup 4) Properties of groups 5) Application to the art in Japan 6) Representation of finite groups 7) Characters  8) Introductive Algebraic Geometry 9) Singularity 10) McKay correspondence. Assignments We will have time for discussion during lecture and exercise at home after lecture. I hope every student enjoys the mathematical discussion with other students and you have to solve the exercise as a report problem.
13	Required readings	I will not use any textbooks during lecture and I will introduce some books or papers which are related with the contents of my lecture for advanced studies.
14	Reference readings	-
15	Notes on Taking the Course	※Students are asked to have their camera turned on during the lecture.

UTokyo Global Unit Courses
International Exchange Group, Education and Student Support Department,
The University of Tokyo, 7-3-1, Hongo, Bunkyo-ku, Tokyo 113-8652 JAPAN

Please send all inquiries regarding the courses to the following email address:

utokyo-guc.adm(at)gs.mail.u-tokyo.ac.jp *Please change (at) to