GUC24S211C | Group Theory and Its Applications

After PhD from the University of Tokyo, I worked as an assistant at Tokyo Metropolitan University and an associate professor at Nagoya University. Since 2017, I have been a professor at the Kavli Institute for the Physics and Mathematics of the Universe at the University of Tokyo. During this period, I also stayed at institutions such as the University of Mannheim, the Institute for Advanced Study in Princeton, and the Newton Institute, actively engaging in education and research. In 2001, I received the Special Prize of Takabe Award from the Mathematical Society of Japan.

Prof. Yukari ITO

1	Subject	Group Theory and Its Applications
2	Field	Mathematics, Art
3	Key words	Group; Symmetry; Art
4	Global Unit	1
5	Lecturer	Yukari ITO
6	Period	July 1 - 5, 2024
7	Time	08:30-10:00, 10:30-12:00 (Japan Standard Time)
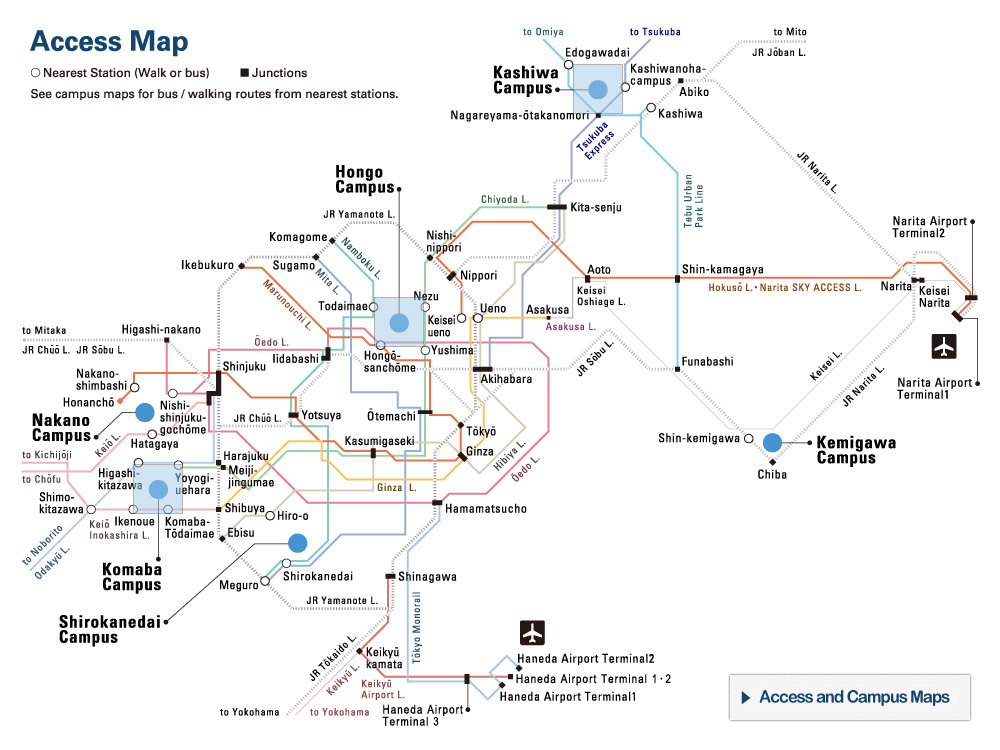
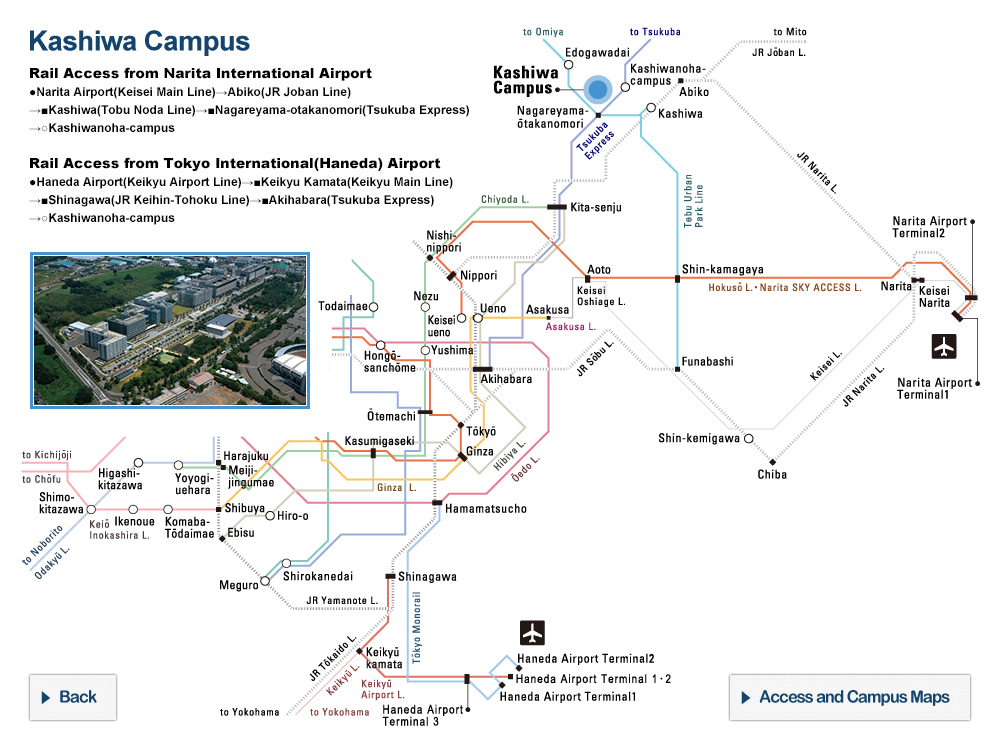
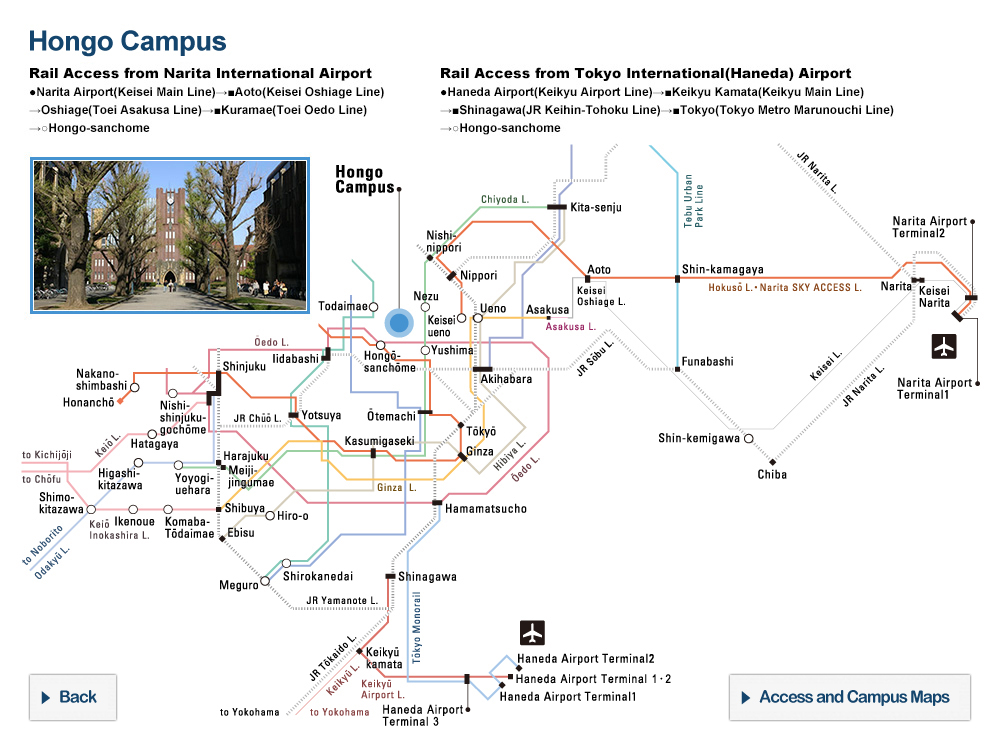
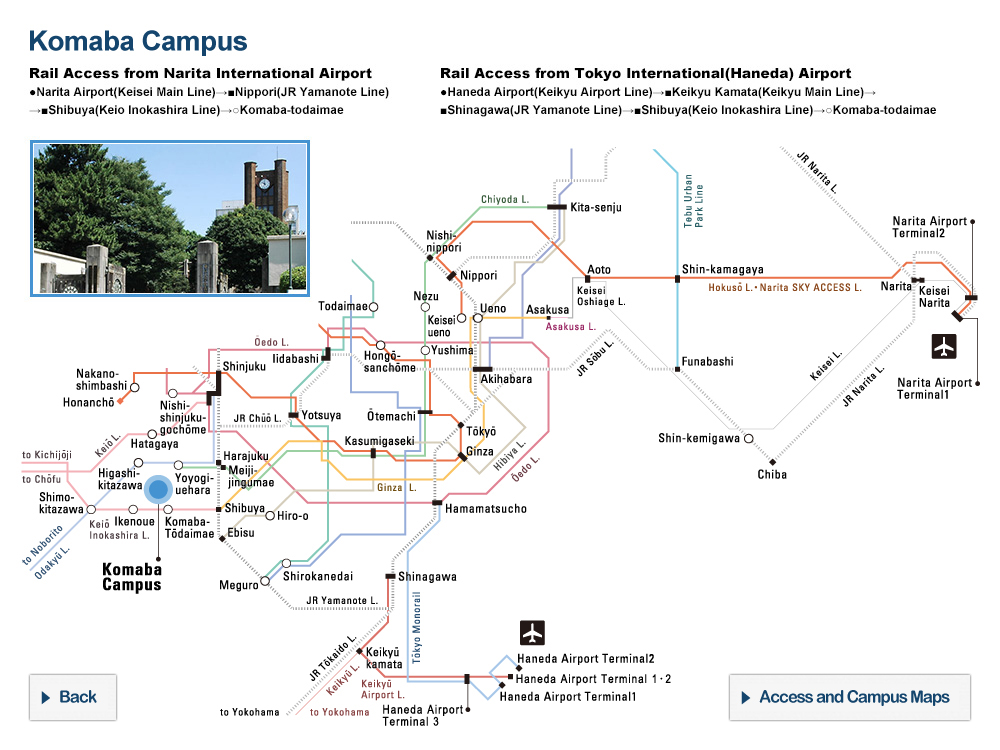
8	Lecture style	In-person (on Hongo Campus)
9	Evaluation Criteria	Excellent (S) 90–100％; Very good (A) 80–89％; Good (B) 70–79%; Pass (C) 60–69%; Fail (D) 0–59％
10	Evaluation methods	Attendance/Participation 30%, Presentation 30%, Final Report 40%
11	Prerequisites	While this is a foundational mathematics course, a basic understanding of linear algebra is recommended.
12	Contents	Purpose Students who successfully complete this course will be able to understand the definition of a group and its easy properties with some examples. Moreover, they will make their own artwork or application in the class. Description Main part of this course is a lecture and exercise in person. I hope we can do discussion, group activities and presentation. Schedule 1-2 Definition of a group and some examples. 3-4 Basic properties of groups. 5-6 Find symmetry with group theory! 7-8 Group representations 9-10 Make your own group! Assignments 90-minutes lecture and 90-minutes activities for 5 days. The activities contain mathematical exercise, presentation and artwork.
13	Required readings	-
14	Reference readings	You can find the mathematical knowledge in any text book on group theory.
15	Notes on Taking the Course	-

UTokyo Global Unit Courses (GUC)
International Education Promotion Group, Education and Student Support Department
The University of Tokyo, 7-3-1, Hongo, Bunkyo-ku, Tokyo 113-8652 JAPAN

For inquiries regarding GUC, kindly direct them to the following email address:
utokyo-guc.adm(at)gs.mail.u-tokyo.ac.jp *Please change (at) to @